In principle, two essentially different representation methods for Boolean functions have been successfully used in logic synthesis software: Cube Calculus (CC), and Decision Diagrams (DDs). Similarly, for multiple-valued logic one uses two representation methods: Multiple-Valued Cube Calculus (Positional Notation) and Multiple-Valued Decision Diagrams. These methods have been also extended to incompletely specified functions.
All these representations are being improved with time, and several variants of them have been invented and proved superior in some applications. For instance, XBOOLE system of Bochmann and Steinbach [2] introduces Ternary Vector Lists (TVLs), a variant of Cube Calculus with disjoint cubes, new position encoding and new operations, and demonstrates its superiority on some applications. Similarly, Functional Decision Diagrams (FDDs), Kronecker Decision Diagrams (KDDs), Algebraic Decision Diagrams (ADDs), Moment Decision Diagrams (MDDs), and other Decision Diagrams (DDs) have been introduced and shown superior to the well-known Binary Decision Diagrams (BDDs) in several applications. In other related efforts: Luba et al [10] introduced a new representation of Rough Partitions and used it in few successful programs for Boolean and multiple-valued decomposition; and Truth Table Permutations to create BDDs are recently investigated [11, 8]. While cubes seem superior in problems with a limited number of levels, such as SOP or ESOP synthesis, the DDs are superior for general-purpose Boolean function manipulation, tautology, technology mapping, and verification.
This paper introduces a new represention of binary and multiple-valued functions. More generally - a representation for discrete mappings and for some restricted class of discrete relations. We call this new representation the Cube Diagram Bundles (CDB). Cube - because they operate on cubes as atomic representations, Diagrams - because they use Decision Diagrams (of any kind) to represent sets. Bundles - because several diagrams and other data are used together to specify a function or a set of functions. CDBs are related to Cube Calculus [7], Decision Diagrams [3], Rough-Partitions [10], and Boolean Relations [4]. This new representation is general and can be applied to both binary and multiple-valued functions (state machines) in the same way. It allows to add and remove variables (functions) in the synthesis process, which would be difficult or inefficient using other representations. All operations are reduced to set-theoretical operations on DDs.
Let us observe that the meaning of a representation in an algorithm is two-fold. First, it allows to compress data - the switching functions - so that the algorithm becomes tractable in time or in space. Secondly, any representation introduces certain bias for function processing, making some algorithms particularly suited for some representations, and less for other. This author believes that it is not possible to create a single represention that will be good for all applications, and the progress of various representation methods in past years seems to support this opinion. Therefore, here we concentrate on an area that has not found sufficient interest until very recently, but one that in our opinion will be gaining in importance: binary and multiple-valued, very strongly unspecified functions. We will call this class SUF - Strongly Unspecified Functions. Such functions occur in Machine Learning (ML) [14], Knowledge Discovery in Databases (KDD), Artificial Intelligence (AI), and also in some problems of circuit design, such as realization of cellular automata. One can observe that many well known problems in logic synthesis can be also converted to binary SUF functions: for instance every multi-output function can be converted to a single output binary SUF (BSUF). SUF functions are manipulated while solving some decision problems and Boolean equations. Also, every multiple-valued input function can be converted to a binary SUF. Multiple-Valued SUF (MVSUF) are important in ML and KDD areas.
One can think about a discrete function as a two-dimensional table - see Table 1, in which
the (enumerated) rows correspond to the elements of the domain
(the minterms) or to certain groups of elements of the domain (the cubes).
The columns of the table correspond to the input and output variables.
Sometimes, also to intermediate (auxiliary) variables which
can be (temporarily) treated as input or output variables.
Let us observe, that such table is in a sense realized
in cube calculus, where the cubes correspond to rows.
The disadvantages of cube calculus include however:
- some large multilevel functions, such as an EXOR of many variables, produce too many cubes after flattening
so that their cube arrays cannot be created,
- it is difficult to add and remove input and output variables to the cubes
dynamically in the synthesis process,
- in strongly unspecified functions we would need relatively few but
very long cubes, - column-based operations are global, and therefore slow.
Luba invented a new function representation called Rough Partitions (r-partitions, or RP) [10].
R-partition is also called a cover.
This representation stores r-partitions 
for all input and output variables 
as lists of ordered lists.
Each upper level list represents an r-partition for variable
, and lower level lists
correspond to the blocks of this partition. A block of partition
includes numbers of
rows of the table that have the same value VAL
in the column corresponding to variable .
For instance, in ternary logic there are three blocks that correspond to values VAL = 0, VAL = 1, and
VAL = 2, respectively.
All operations are next performed on these r-partitions using
r-partition operations that
extend the classical Partition Calculus operations of product, sum and relation 
of Hartmanis and Stearns.
Blocks included in other blocks are removed, and the origination of a block - which value of
input variables it comes from - is lost.
This makes some operations in this representation not possible, and some
other not efficient.
Our other source of inspiration
is the concept of Generalized Don't Cares [15].
In binary logic, a single-output
function F has two values: 
and 
, and there exists one don't care 
that corresponds to a choice of these two values.
Analogously, in a three-valued
logic, function F has three values: , , 
and there exist the
following combinations of values: , 
, 
, and 
.
The last one corresponds to a classical don't care, but the other three are new,
and we will define them all as the generalized don't cares.
Similarly, the concept of generalized don't cares can be applied to k-ary logic
for any value of k. This concept has applications for instance in Machine Learning and
Knowledge Discovery from Databases.
It has also some link to Boolean Relations.
In this section, a multi-valued, multi-output function F with generalized
don't cares will be referred to as a function.
In CDB representation, function F is represented as a record of:
1. A pointer to a list Var(F) of primary input variables on which the function depends. The variables are sorted lexicographically.
2. A pointer to a list Inp(F) of vectors of primary input columns. The vectors are in the same order as the input variables. Each vector has as many positions as the corresponding variable has values, and the positions are sorted starting from 0 to k-1, where k is the number of values. Each position of the vector is a pointer to a DD. These are called "input value DDs."
3. A pointer to a list Out(F) of vectors of output columns. This list is analogical to the Inp(F) list. The DDs in the vectors in this list are called "output value DDs." The "input value DDs" and the "output value DDs" are called "value DDs".
The representation of Luba has been used only for decomposition, and CDBs are a general-purpose function representation designed for speed and data compression - there are then several differences of CDBs and the representation of Luba. For efficiency of operations, the CDB of F stores also the list of primary input variables on which F depends (some of them can be still vacuous). It stores vectors of function values, and not rough partitions. This means, inclusion operations on blocks are not performed, and we keep track on the origin of each block - what value of the variable it corresponds to. In case of cofactors, we store then cofactor functions, and not their equivalence classes. CDBs represent functions with generalized don't cares, while Luba represents only classical don't cares. The rows (their numbers) correspond in Luba's approach to minterms or arbitrary cubes, while they correspond to disjoint cubes in CDBs. All sets are represented as ordered lists in RP and as Decision Diagrams in CDBs. Currently we use standard BDDs, but any kind of decision diagrams can be used, and we plan to test other DD packages in the future. Because the sets are represented as DDs, CDBs introduce new variables to realize these DDs with. They are called the secondary input variables. The number of these variables is usually much smaller than the number of primary input variables, and the complete freedom of encoding rows with these new variables allows to minimize the size of all BDDs. This property is totally missing in Rough Partitions and exists only in [11, 8]. While the authors from [11, 8] solve it as a truth-table permutation problem, we solve it as a cube encoding problem, which is more general.
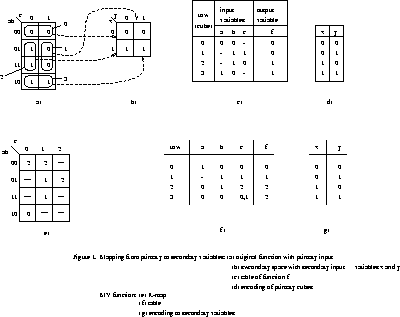
Example 1: Tables and encodings of functions. The first example illustrates a table and encoding for a binary-input, binary-output completely specified function. A Kmap with primary input variables a, b, and c is shown in Fig. 1a. This table has four disjoint cubes. Two are OFF cubes, enumerated 0 and 1, and two are ON cubes, encoded by 2 and 3. As the results of encoding of primary cubes with secondary input variables, x and y, a new map from Fig. 1b is created. Figure 1a,b shows clearly how cubes of the first map are mapped (encoded) to the minterms of the secondary map. The table for the function from Fig. 1a is shown in Fig. 1c, and the encodings of its rows to secondary input variables is shown in Fig. 1d. The function is specified as the following CDB.
Var(F) = {a,b,c}. Inp(F) = { [ pointer to BDD for {0,1,2}, pointer to BDD for {1,2,3} ], [ pointer to BDD for {0,3}, pointer to BDD for {1,2} ], [ pointer to BDD for {0,2,3}, pointer to BDD for {0,1,3}]} ;;var. a,b,c
Out(F) =
{[pointer to BDD for {0,1}, pointer to BDD for {2,3}]}
The second example, see Table 1, presents a table for a binary-input, 5-valued-output incompletely specified function with generalized don't cares. The map for this function is in Fig. 5a. In this case:
Out(F) = { [ pointer to BDD for {0,2,3,4,5,6,8}, pointer to BDD for {0,1,7,8,10}, pointer to BDD for {1,9,11}, pointer to BDD for {3,4,6,7,9,11}, pointer to BDD for {5,10} ] } ;;;;;; for 5-valued output variable f.
The third example presents a table, Fig. 1f, for an incompletely specified function with standard don't cares from Fig. 1e. It has two binary input variables, a and b; a ternary input variable c, and a 3-valued-output. The encoding of primary cubes with secondary input variables x and y is shown in Fig. 1g.
The function is specified as the following CDB.
Var(F) = {a,b,c}.
Inp(F) = { [ pointer to BDD for {1,2,3}, pointer to BDD for {0,1} ], [ pointer to BDD for {0,3}, pointer to BDD for {1,2} ], [ pointer to BDD for {0,3}, pointer to BDD for {1,3}, pointer to BDD for {2} ] }
Out(F) = { [ pointer to BDD for {0}, pointer to BDD for {1}, pointer to BDD for {2,3} ] }
The following points about CDBs are important:
1. Standard don't care positions are not stored in tables and CDBs, but generalized don't care positions are stored.
2. The definitions of a Binary Cube Diagram Bundles and Multiple-valued Cube Diagram Bundles (mvCDBs) are exactly the same. Therefore, the same operations are applied to them.
3. All Boolean operations on CDBs can be easily realized as set-theoretical operations on corresponding DDs.
4. The important concept of a cofactor is calculated using only the set-theoretical operations as well: cofactor CF of F with respect to cube C is calculated as follows:
CF := DD(F) 
DD(C), 
:= Var(F)-Var(C).
5. The operations of derivative, differential, minimum, maximum, k-differential, k-minimum, and k-maximum of a function [2] are also realized. Since all these operations are based on set and cofactor operations, they can be easily realized because of points 2 and 3 above.
6. A CDB represents a set of cubes. Each true minterm in DD(F) is an ON cube in function F on primary variables, and each false minterm in DD(F) is an OFF cube.
7. There is no difference in the representation of primary input variables,
auxiliary variables and output variables.
Therefore, CDBs are good to represent functions defined on combinational functions
of input variables, one can just
add new "columns", which means, new sets of "value DDs".
For instance, to check a separability
of a function to unate functions,
one just introduces new input variables, like 
= 
.
Similarly, one can create new intermediate variables such as 
= 
, 
= 
,
or 
= 
by calculationg corresponding functions on BDDs of
a and b and storing new items in Var and Inp.
This property allows also to:
realize algorithms that operate on output functions as on variables;
use auxiliary functions for synthesis; and re-use the existing functions in synthesis.
8. We created one more variant of CDBs, that we call encoded CDBs, or ECDBs.
For instance, when there are four values of variable , the standard CDB would create
four DDs for this variable. However, the ECDB would create only two "encoded" DDs.
This obviously saves space.
Operations on
ECDBs are very similar to those on CDBs, but will be not discussed here [15].
9. During the incremental reading of the input data in the form of disjoint cubes of primary variables (rows of the "table"), the encoding of these primary cubes as minterms in the new space of secondary variables is executed. The goal of this encoding is to simplify all DDs of the CDB. This is done in such a way that the false minterms that are encodings of all primary OFF cubes are grouped near the cell 0...0 (the minimum minterm in the space of new variables). Similarly, true minterms of new space that are the encodings of all primary ON cubes are grouped near the cell 1...1 (the maximum minterm in the new space). In addition, the larger the cube, the closer it should be located to the minimum or the maximum cell, respectively. Moreover, the cube encoding algorithm attempts to fill those cubes in the new space that are of smaller Hamming distances with either the minimum or the maximum minterm, in such a way that as many as possible of these cubes become completely filled with the same types of minterms. This is done for all DDs in parallel.
