Basic Decompositions are Curtis Decomposition and
PUB Decomposition [15]. They happen more often than Immediate Decompositions.
Hower, when executed with large value of Multiplicity Index 
they lead to
difficult encoding problems and the not necessarily minimum circuits
(especially that we are never able to perform exhaustive search of sets A, B and C).
We execute, therefore, these decompositions only with small values of = 3,...8.
Because of lack of space, we present only the Curtis Decomposition:
F = 
where G is a 
-output function.
Following the approach from [16],
given the bound set 
and the free set 
,
first a fast approximate graph coloring of the
Column Incompatibility Graph (CIG)
is found with the nodes corresponding to columns, and the edges to
incompatible pairs of columns. Compatible are columns that
can be combined (can be completed to the same pattern).
Next the encoding method that is similar to the input encoding algorithm for function H from [16]
is applied, but which attempts to minimize both H and G.
Finally, functions G and H are found.
The reason to use here graph coloring instead of Clique Partitioning is to dramatically decrease the size of the memory. Let us assume that the N columns of the covering table correspond to the columns of the RVM, and the rows of the covering table correspond to the maximum cliques. Thus, for strongly unspecified functions, the number of rows is exponential, while the graph has only N * (N-1) / 2 edges.
A set covering algorithm is well known that makes use of essential rows, secondary essential rows and dominations of rows and columns. In case of non-cyclic covering tables, this algorithm finds the exact solution without backtracking. We will present a similar algorithm for graph coloring of the CIG. Node G2 of the graph is dominated by node G1 if the set of incident nodes of G1 includes (properly or not) the set of incident nodes of node G2. In such case, any color of node G1 can be also applied to node G2. Thus, this fact can be stored, and the node G2 can be removed from the graph, together with all its incident edges. This leads to a new graph, that can possibly have new dominated nodes, and so on, until the graph is reduced to a complete graph, for which every node is colored with a different color. When there are no dominated nodes in the graph (this is a cyclic graph, a counterpart of a cyclic set covering table), a coloring choice is done as in [16]. This can lead to dominated nodes, and the node dominations are propagated and removals are done as presented above, until a new branching choice is necessary. There is a perfect analogy of this coloring approach with the popular methods of solving both cyclic and non-cyclic covering problems, but our approach is faster and does not require creating large covering tables. Moreover, it was found experimentally that most CIG graphs are non-cyclic.
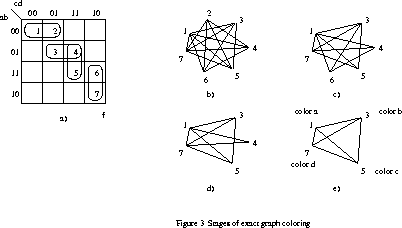
Example 3.
We will illustrate how to convert the covering
problem to the coloring problem using a Kmap of a non-cyclic function f, Fig. 3a.
Numbers denote the true minterms. All other cells are false minterms.
Obviously in this case, after sharping essential primes
and 
,
the secondary essential primes 
and b c d are created.
After sharping these secondary essential primes
no true minterms remain, so the exact solution was found for a non-cyclic
function f without backtracking.
The Incompatibility Graph (IG) corresponding
to this map is shown in Fig. 3b. The stages of coloring the graph are
shown in Fig. 3b - 3e.
In Fig. 3b node 2 has neighbors 4,5,6,7, and node 1 has neighbors 3,4,5,6,7.
Therefore, node 1 dominates node 2, and 2 is removed from the graph,
leading to the graph from Fig. 3c. Now node 6 has neighbors 1,3,4 and node
7 has neighbors 1,3,4,5. Thus node 7 dominates node 6 and node 6 is removed.
This leads to the graph from Fig. 3d. Now node 3 has neighbors 1,5,7 and node 4 has
neighbors 1,7. So, node 3 dominates node 4 and node 4 is removed.
Now, Fig. 3e, the graph is a complete graph. Its nodes are colored with different colors,
as shown. With respect to dominations, node 2 is colored with the same color as node 1, which is
, node 4 is colored with 
, and node 6 is colored with 
.
In CIG, columns of nodes colored with the same color are combined as compatible groups of
columns which determines column partitioning and the value of .
In some covering problems, like in SOP minimization, a group of CIG nodes colored
with the same color are not necessarily all compatible, and group compatibility
must be checked [5]. It can be proven, however,
that in the Column Compatibility Problem in Functional Decomposition
(for both binary and mv cases),
if columns in a set are pairwise compatible
the set of all these columns is compatible as well [15].
Then the solution from CIG coloring is always correct.
This is, however, no longer true for mv functions with the generalized don't cares [15].